谷口研究室
| 指導教員 | 谷口健二 教授 |
|---|---|
| テーマ | 微分方程式の表現論による研究 |
研究内容
群とは抽象的には掛け算と割り算がうまくできる集合のことですが、具体的な対象としては、直交行列全体の集合や、1 から n までの整数の置換全体の集合のように、ある集合や空間上の変換として現れることが多く、様々な物や現象の対称性を数学的に記述するものです。
ある群の持つ対称性や性質を、線形空間上の線形変換として表すことを表現といいます。表現論とは、文字通り表現に関連した研究を行う分野のことであり、
- 表現自体の研究
- 群と表現を使って様々な空間や方程式を解析すること
- 逆に,群と表現を使って面白い空間や方程式を構成すること
- 現象に隠された対称性を見つけ出すこと
などが目標として挙げられます。
一口に「表現論」といってもその領域は広く、代数・幾何・解析・数理物理など、数学の関わるほとんど全ての分野と共有点を持ちますが、私は群の表現から構成される微分方程式系に興味を持っています。近年、私はその中でも特にWhittaker 関数という、ある表現から定まる微分方程式系の解空間上に実現される実簡約型リー群の表現の組成列について研究を行っています。
この研究に関しては、標準 Whittaker (g,K)-加群と呼ばれる表現を定義し、その構造解析を行っています。その結果、まずは構造が簡単な場合である、無限小指標が generic なときの構造を決定しました。無限小指標が integral な場合についても、U(n,1) や Spin(n,1)、SL(3,R)、Sp(2,R) といった低階数の群の場合に構造を完全に決定しました。
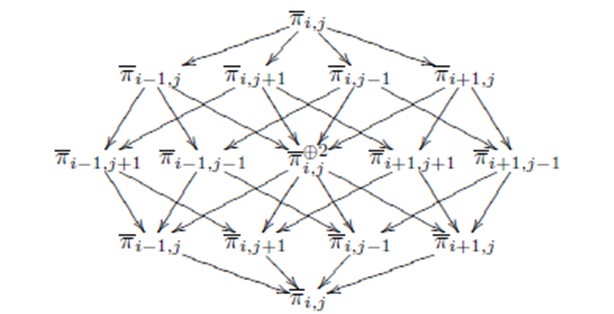
左図は U(n,1) の(一般化)標準 Whittaker (g,K)-加群の構造を表すグラフです。
参考文献
- Kenji Taniguchi, On the composition series of the standard Whittaker (g,K)-modules
- Trans. Amer. Math. Soc. 365 (2013), 3899--3922.
研究者情報

| 教授:谷口健二 | |
| 学位 | 博士(数理科学) |
| 所属学会 | 日本数学会 |
| 研究分野 | リー群の表現論 |
