中田研究室
| 指導教員 | 中田行彦 准教授 |
|---|---|
| テーマ | 微分方程式のダイナミクス、数理生物学 1.感染症の数理モデル 2.時間遅れをもつ微分方程式のダイナミクス |
研究内容
時間とともに状態が変化する物事は我々の身の回りに多く存在します。多くの物事が時間とともに変化することがよく知られる一方で、その予測や対策が困難な場面が多々あります。感染症の流行や体内の疾患、生態系の変動、天候や景気の変化はそのような例で、身の回りには、「何故それがそのように変化しているのか」わからない現象が多く溢れています。
我々は、現象を記述する数理モデルを、数学理論やシミュレーション、分野を超えた共同研究によって解析し、実現象への洞察を獲得することを目指しています。数理モデルから知りたい情報を抽出するには数理的に困難な課題も多く、従来と異なる新たな視点が求められることも多々あります。現象に動機づけられる数理モデルの研究と共に、関連して現れる数理的な現象の解明を行い、広い視野を獲得し、諸問題の解決を目指しています。
感染症の数理モデル
感染症の流行には、様々な興味深い現象が見られます。周期的な流行を繰り返す感染症や、薬剤に対して耐性をもつウイルス、感染後にホストの体内に居座り続け、いつ再発するか分からないような病原体、ホストの免疫低下によって再感染が起こり、それが次の流行の引き金となるような感染症、複数の病原体が作り出すような複雑な流行現象など。感染症の流行現象を、複雑でマルチスケールな非線形力学系として捉え、現象のメカニズムを理解することを目指しています。
下の微分方程式は、感染症に対して感受性を持つ人口と現在感染している人口の時間変化を微分方程式で表した簡素な数理モデルです。一度免疫を保持した個体も、時間の経過とともに、免疫を失って、感受性保持個体となるところがモデルの特徴になっています。
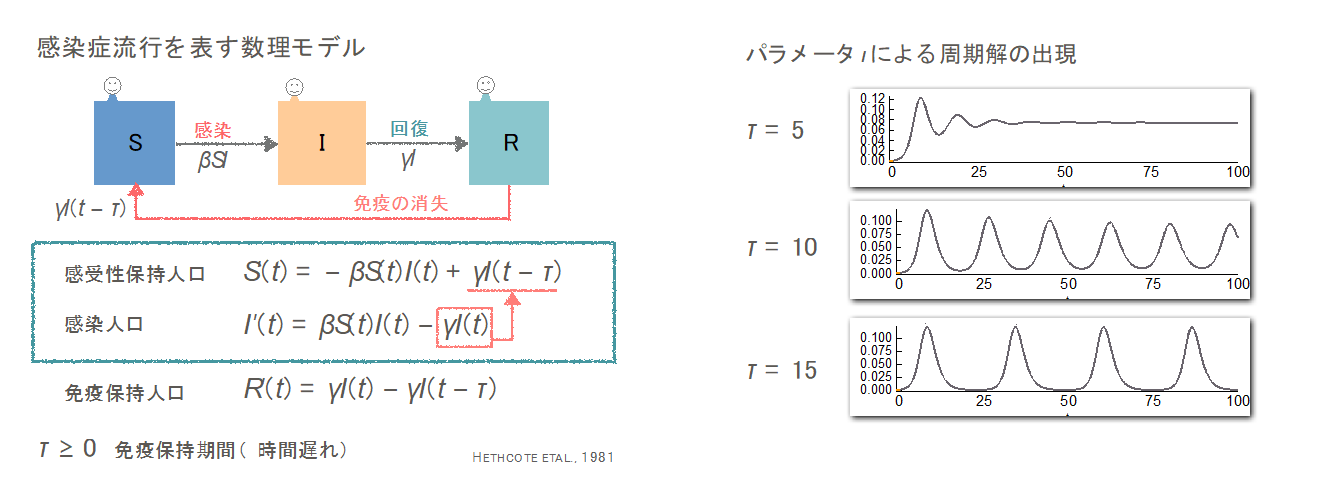
上の図はモデルのパラメータの増加とともに、周期的な振動解が出現することを表した数値シミュレーションの結果で、個体の免疫低下から、感染症の周期的な流行が引き起こされる可能性を示唆しています。どのような条件下で、周期的な流行が引き起こされるのか、数理モデルから流行の周期や規模について洞察を得られないか、また数値シミュレーションでは観察し難いようなダイナミクスがありえないか等、力学系理論や微分方程式の理論を手掛かりにして調べています。感染症の流行周期が、個体の免疫保持期間とどのように関連しているか調べることは最近の研究のテーマの1つです。また最近の研究では、個体の感受性分布と再感染によって、(再感染を考えないような)従来の数理モデルでは予測が困難な流行現象が起こり得ることを見つけました。
時間遅れをもつ微分方程式のダイナミクス
人口動態や生物現象を表す数理モデルでは「時間遅れ」の理解が大変重要なものとなっています。細胞の増殖を思い浮かべてみると、分裂した細胞が、また分裂するためには、細胞の成長や染色体の複製のために時間が必要となっています。人間も同様で、生まれた人間個体がすぐさま新生児を産むことは出来ず、個体の再生産には、個体の成長期間が必要で、「タイムラグ」が必然と生じます。感染症の流行動態では、新規感染者の再生産に、必然と時間遅れが生じます。また、明るさに反応して、瞳孔の大きさが変化することで、暗闇に次第に目が馴れるなど、生物は、物事を知覚してから、反応するまでに時間が必要です。
時間遅れをもつ微分方程式の定性理論が前世紀に大きく発展しましたが、簡単に見える方程式でも解の挙動について理解が進んでいないことも多く、今でも問題が沢山残っています。時間遅れの微分方程式の解のダイナミクスは、無限次元の関数空間で理解することが自然ですが、その無限次元性が、解挙動の細やかな理解を困難でありながら面白い問題としています。我々は、従来得られてきた数学理論を適用するのみならず、解析手法の整備を行いながら、時間遅れをもつ微分方程式の性質を調べています。最近では、微分方程式の周期解や有限時刻での爆発解、異なるタイムスケールから生まれる2相のダイナミクスなど、時間遅れがあるからこそ現れるような非線形現象を数理的に理解することに取り組んでいます。
研究者情報

| 准教授:中田行彦 | |
| 学位 | 博士(理学) |
| 所属学会 | 日本数学会、日本応用数理学会、数理生物学会 |
| 研究分野 | 微分方程式論、数理生物学 |
