津田研究室
| 指導教員 | 津田照久 教授 |
|---|---|
| テーマ | 数学、複素領域の微分方程式 |
研究内容
専門は複素領域の微分方程式論です。とくにソリトン方程式やパンルヴェ微分方程式、いわゆる完全積分可能系(可積分系)と呼ばれる対象に興味を持っています。可積分系の持つ解析学と代数幾何や表現論、組合せ論など様々な数学の不思議な調和と、何より問題意識が古典的であることに魅力を感じています。
ゼミナールでは指導教員の専門に拘らずに、広く数学や数理物理学の中からテーマを選びます。数学的なものの考え方を通して、論理的な思考力や柔軟性を身につけることも目標の一つです。基礎から始めて、一人一人の興味に応じた研究へと進みます。大学1・2年生のときは数学に限らず物理、化学、生物など自然科学全般に関心を持って学ぶことも大切です。
些か専門的になりますが、具体的な研究内容について紹介します。
ソリトン方程式などの無限次元可積分系の研究
シューア函数の一般化に、ヤング図形の組に付随する普遍指標(universal character)があります。シューア函数が一般線形群の既約多項式表現の指標であるのに対し、普遍指標はその既約有理表現の指標を与えます。
一方、シューア函数は表現論のみならず、可積分系の理論とも結びついています。事実、佐藤幹夫氏ら京都スクールの歴史的発見が明らかにしたように、最も重要なソリトン方程式のクラスであるKP階層は、シューア函数の特徴付ける無限可積分系に他なりません。
では、普遍指標の特徴付ける無限可積分系は一体何なのか?この問題を解決したのが論文[T04a]です。新しく導入した無限可積分系はUC階層と呼ばれ、KP階層の自然な拡張を与えます。解空間は佐藤グラスマン多様体の直積を成し、とくに斉次多項式解は普遍指標に一致します。これは表現論に現れた普遍指標に対し、微分方程式による再定義を与えた意味でも興味深い結果といえます。
パンルヴェ方程式などの非線形微分方程式が定める特殊函数の研究
微分方程式で定義される新しい特殊函数を探そう!このスローガンのもと、楕円函数の一般化を目指したパンルヴェは、2階代数的常微分方程式の中で、動く特異点が高々極であるものを分類しました。その一覧表から既知の函数で解けるものを除いた6つの非線形常微分方程式をパンルヴェ方程式と呼びます。
一般にパンルヴェ方程式の解は超越的な函数(=新しい函数)を定義します。一方、パラメータが特別な場合にはガウス、クンマー、エルミート、ベッセル、エアリーの名を冠した超幾何函数とその合流型を特殊解として含みます。鑑みてパンルヴェ方程式は、古典的な特殊函数の満たす方程式の非線形拡張と看做せます。
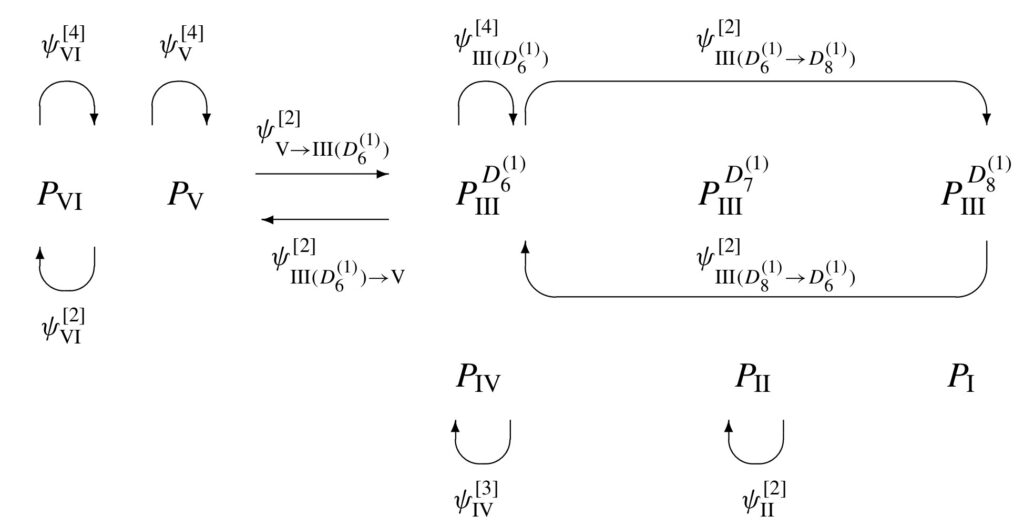
数学史的にも興味深い発見から120年、今やパンルヴェ方程式の研究は一望するのも難しいほど多岐に発展を遂げています。論文[T14]ではUC階層の相似簡約を経由して、線形常微分方程式のモノドロミー保存変形であるパンルヴェ方程式と普遍指標との関係を明らかにしました。パンルヴェ方程式の性質:ラックス形式、タウ函数と双一次形式、ワイル群対称性、特殊解などが、無限可積分系の観点から統一的に理解できる点が肝心です。
 |
 |
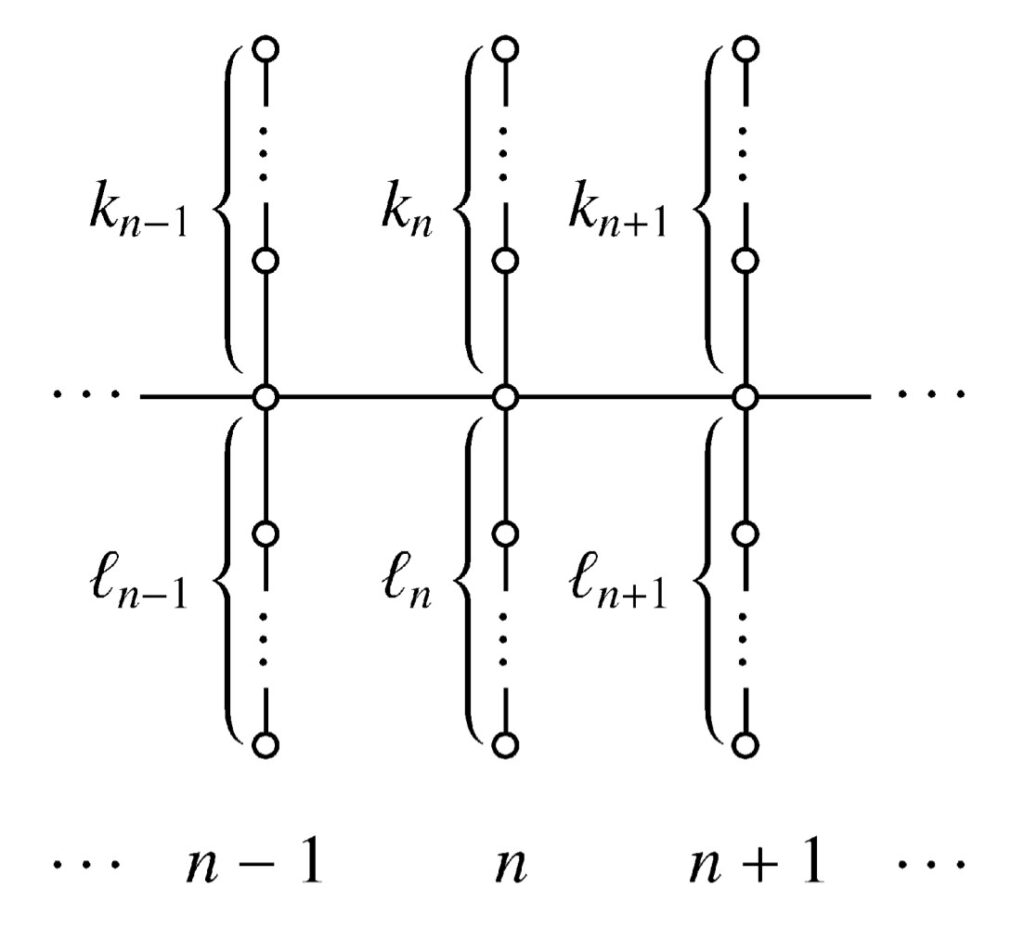
| 論文[TOS05]ではパンルヴェ方程式の代数的な変数変換による対称性(折り畳み変換)を曲面の代数幾何を用いて完全に分類しました。 | 論文[MT17]では「ベクトル連分数展開」あるいは「エルミート・パデ近似」から線形常微分方程式の離散対称性を導きました。パンルヴェ方程式の行列式構造の一つの由来です。 |
 |
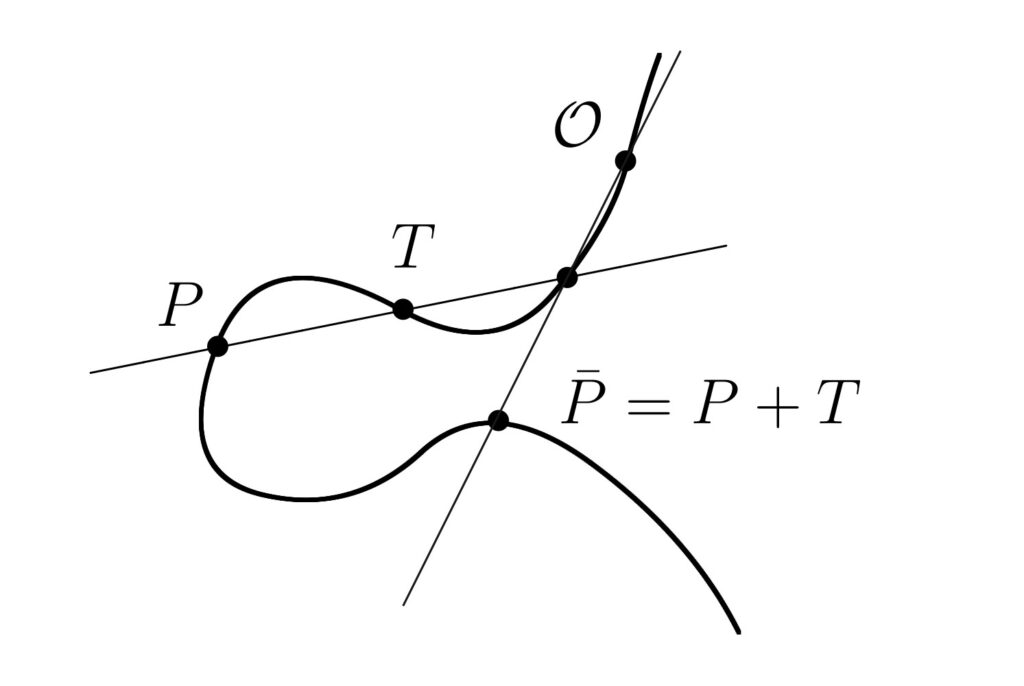 |
| 論文[TT09]では有理代数多様体上にワイル群の双有理作用とタウ函数を構成しました。アフィン型の場合に平行移動から生ずる離散力学系がq-差分パンルヴェ方程式です。 | 論文[T04b]では(パンルヴェ方程式の離散版を含む)可積分な離散力学系の雛形として広く研究されてきたQRT写像に対し,有理楕円曲面の加法公式による記述を与えました。 |
参考文献
- [T04a] T. Tsuda, Universal characters and an extension of the KP hierarchy, Comm. Math. Phys. 248 (2004) 501–526.
- [T04b] T. Tsuda, Integrable mappings via rational elliptic surfaces, J. Phys. A: Math. Gen. 37 (2004) 2721–2730.
- [TOS05] T. Tsuda, H. Sakai and K. Okamoto, Folding transformations of the Painlevé equations, Math. Ann. 331 (2005) 713–738.
- [TT09] T. Tsuda and T. Takenawa, Tropical representation of Weyl groups associated with certain rational varieties, Adv. Math. 221 (2009) 936–954.
- [T14] T. Tsuda, UC hierarchy and monodromy preserving deformation, J. reine angew. Math. 690 (2014) 1–34.
- [MT17] T. Mano and T. Tsuda, Hermite–Padé approximation, isomonodromic deformation and hypergeometric integral, Math. Z. 285 (2017) 397–431.
研究者情報

| 教授:津田 照久 | |
| 学位 | 博士(数理科学) |
| 所属学会 | 日本数学会 |
| 研究分野 | 複素領域の微分方程式、特殊函数 |
